|
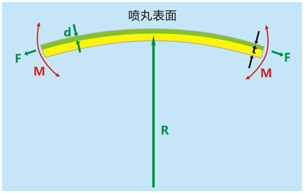
噴丸中影響阿爾門弧高值的試片主要因素阿尔门弧高值是阿尔门试片中心位置的弯曲值。该弯曲是由高速弹丸轰击阿尔门试片的一個面之后产生的,用于喷丸束流的“强度”测试。弧高值是一個非常重要的指标,在一些标准例如SAE J442和J443的标准中均有所提及。 噴丸後的阿爾門試片從阿爾門固定器上取下之後,會形成一個彎曲的形狀,如圖1所示。弧高值會隨著曲率1/R的增加而增加。噴丸會産生一個深度爲d的壓應力層。該應力層中的壓應力作用在阿爾門試片的橫截面,産生了一個力F。同時在試片上施加了一個彎矩M。試片抵抗彎矩的能力取決于其彈性模量、寬度和厚度t。
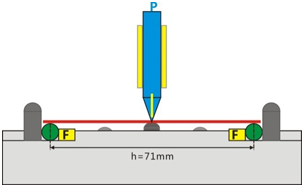
影響阿爾門試片弧高值的有關試片的因素如下: (1)試片的彎曲抗力,E*I。其中E爲彈性模量,I是剛度系數(同時也稱爲試片的斷面慣性矩); (2)引入的彎矩,M。試片的抗彎強度越大,其噴丸後的弧高值越小。噴丸引入的彎矩越大,試片噴丸後的弧高值越大。 本篇文章對影響抗彎強度的試片因素和彎矩進行可分析。阿爾門試片的可靠性和一致性需要對以上要素進行控制。 試片的彎曲模型 基本梁的彎曲理論給出了施加于梁上的彎矩和由該力矩引起的曲率1/R之間的關系: 1/R=M/(E*I) (1) 其中R是彎曲半徑,E是彈性模量,I是試片的斷面慣性矩,M是施加在試片上的彎矩。 公式(1)表明,試片的曲率(或弧高值)隨著彎矩的增加而增加,但隨著彈性模量和斷面慣性矩的增加而減小。彎矩和彈性模量是常見的參數,端面慣性矩相對來說不太常見。端面慣性矩是梁的剛性定量表征方式。幸運的是阿爾門試片的形狀爲矩形,其端面慣性矩I和尺寸之間的關系比較簡單: I=w*t3/12 (2) 其中,w是試片的寬度,t是試片的厚度。 我們可以通過彎曲尺子的方法來更好地理解公式(2)。我們在一個方向上可以容易地彎曲尺子,然而把尺子旋轉90°,我們就會發現很難讓尺子發生明顯彎曲了。 把公式(2)代入到公式(1)中,可得: 1/R=12M/(E*w*t3) (3) 曲率並非弧高值,所以我們需要知道他們兩者之間的關系。采用“相交弦定理”可得: h=s2/(2R) (4) 其中h是弧高值,s爲阿爾門測具上支撐球之間的距離。 把公式(4)中的R代入到公式(3)中可得: h=6s2*M/(E*w*t3) (5) 公式(5)是一個“定式方程”,表征了试片所有重要参数的内在关系。S是阿尔门测具的一個参数,M是丸料冲击和试片变形的函数,E是试片的重要参数,但是受到的关注却不多,w是试片的宽度, t是试片的厚度,w对弧高值的影响远小于t。 阿爾門試片的抗彎強度 阿爾門試片的抗彎強度与E*I成正比,如公式(1)所示。對于给定厚度的N、A和C型阿尔门试片,E和I应该是保持不变的常量。尽管E*I是阿尔门试片的重要参数,但是却很少被直接监测。 把数显的阿尔门测具进行简单的改造就可以用于估算E*I。该简单的改造如圖2所示,其中5.5mm直径的钢杆用于支撑受到载荷为P的阿尔门试片。该钢杆可以避免被施加载荷的阿尔门试片与支撑球之间的接触,进而可以消除它们之间产生过多的磨损。在弯曲的试片接触支撑球之前,可以监测到最大达到0.700mm的弯曲值。钢杆之间的距离最大可为71mm,并在F处使用垫片,目的是要获得最大的弯曲敏感度。适用梁的弯曲公式如下所示: h=(p^* s^3)/(48E^* I) (6)
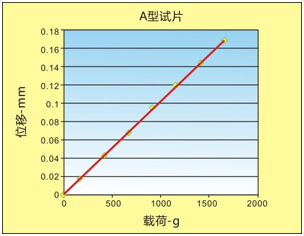
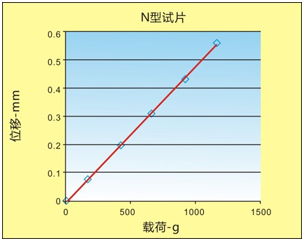
把假定的数值s、E和I代入到公式(6)中可知,對于N型阿尔门试片的弯曲值范围,施加载荷P的范围为1~10N(大约0.1~1Kg)已经足够。圖2中的载荷P可以使用很多种方法实现。本文中所用到的方法就是使用垂直于阿尔门试片的不同质量的铁杆,该铁杆的一端为锥形,锥形顶端与载荷中心线重合。该特殊制作的阿尔门测具需要被支撑,以保证阿尔门试片在两個方向上均水平。 公式(6)表明弯曲值h和所施加的载荷P之间有着直接的关系。该改造后的阿尔门测具可以对一個A型阿尔门试片施加不同的载荷来进行验证。圖3显示了弯曲值和所施加的载荷之间有着非常好的线性关系。
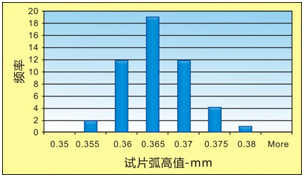
采用改造后的阿尔门测具可以进行许多测试。最重要的商业用途就是测试试片抗弯强度的一致性。学术上的测试包括不同厚度的N、A和C型阿爾門試片的抗彎強度的对比以及弹性模量的测试。 一致性測試 例如,可以在一盒共50個N型阿尔门试片上进行一致性測試。在每個试片的中心位置上均施加相同的758g(7.44N)载荷。其弯曲值在改造的TSP-3型号的阿尔门测具上进行测试。收集到的数据以条形圖的格式呈现,如圖4所示。
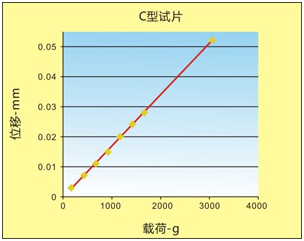
對于给定的P和s值,公式(6)显示弯曲值h和抗弯强度EI之间存在着直接的线性关系。如果h 的变化性越大,那么EI的变化性也越大。 在本次测试中,50個弯曲值的标准差为0.0052mm,平均值为0.3633mm,范围为0.355到0.376mm之间。 阿尔门试片的厚度對于抗弯强度的影响 如果E、P和w是恒定值的話,試片厚度對抗彎強度的影響可以很容易地確定。通過公式(5)我們可知,彎曲值h1/h2和阿爾門試片的厚度t1和t2的關系如下: h1/h2=(t2/ t1)3 (7) 施加同样的758g的载荷后,N型和A型试片的弯曲值分别为0.360和0.079mm,而其厚度分别为0.784和1.293mm(基于每种试片的十次不同位置的测试)。因此h1/h2为4.56,(t2/ t1)3为4.49。差异为1.5%,要比试验误差更大。通过测试发现这两种试片的宽度是一致的,同时所施加的载荷也几乎是一致的,那么造成变化性的因素只剩下弹性模量,E。 彈性模量對抗彎強度的影響 抗弯强度是与试片材料的弹性模量成正比的。阿尔门试片是由材料为SAE 1070的轧制钢带制作而成的,其规定的弹性模量为201Gpa,要比文献上记载的铁素体钢的210MPa的平均值要小4.5%。SAE 1070可以通过冷轧、热轧或窄带材制成。文献上记载SAE 1070材料的测试数据为190~219.4GPa之间。 人們普遍不認爲軋制剛的彈性模量是矢量(即同時具有大小和方向)。而軋制剛是各向異性的,因爲在加工時其晶粒有著擇優定向。該各向異性隨著軋制的程度增加而增加,且寬試片的各向異性要高于窄試片。而中間退火的頻次影響了擇優取向的程度。多次熱軋工藝所産生的擇優取向程度相對來說非常輕微。N型和A型阿爾門試片在熱處理之前通常采用縱切剪邊的寬軋制板材制造而成。而一些C型阿爾門試片是由熱軋板材制造而成。 弹性模量的各向异性直接影响着抗弯强度。接下来就通过一些有限的试验来测试单個随机挑选的N、A和C型阿尔门试片的弹性模量。采用最佳拟合的方法测试通过原点的h/p直线的斜率,并对试片的宽度和厚度进行细致的测试。弯曲值与载荷的相关关系如圖3、圖5和圖6所示。對于不同的阿尔门试片的测试结果如下所示: N型阿爾門試片:E=199.9GPa;A型阿爾門試片:E=204.5GPa以及C型阿爾門試片:E=194.8GPa。 从以上三個测试值可以看出,弹性模量以及相应的抗弯强度差异非常明显。
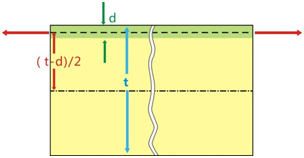
噴丸所引入的彎矩 阿尔门试片受到喷丸后会在其表面上产生一個压应力层。该层上的应力乘以其作用的面积就得到了力F。该力F继而会引入一個弯矩M。阿尔门弧高值h是与弯矩成正比的,如公式(5)所示。 彎矩的産生模型 弯矩的一個简单的产生模型如圖7所示。该弯矩假设是由一個力F产生,其作用的压应力层深为d,那么该弯矩为F(t-d)/2。该力F假设是由压应力层的一個平均应力σ乘以其作用面积(试片的宽度w乘以深度d),那么F=σ*w*d,继而力矩M可以由如下公式表示: M=σ*w*d*(t-d)/2 (8) 阿尔门试片的宽度w和厚度t均是常量,那么公式8中只有两個变量。圖8显示了對于A型阿尔门试片(宽度为18.95mm,厚度为1.295mm)其应力层深度和应力水平對于弯矩的影响。当压应力层深达到试片厚度的一半时,其弯矩达到了最大,然后弯矩一致降低直到整個试片的截面均为压应力时降为零。后面会进一步说明,在实际应用中通常会对强度进行一個严格的限制,所以一般情况下压应力层的深度是不会超过0.2mm,因此弯矩是和平均的压应力水平成正比的。
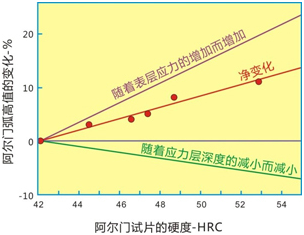
试片材料的性能對于弯矩的影响 影響彎矩的主要力學性能是硬度。一方面,材料更高的硬度會導致噴丸後凹坑的尺寸更小,因此其壓應力層d也會更小。另一方 目前,已经有相当多的试验表明喷丸后材料中的压应力面,更高的硬度也会在压应力层中带来更大的压应力水平σ。因此,我们可能会得到相反 的结果。σ会随着金属材料的硬度增加而增加。但这种精确的关系还未在阿尔门试片上进行建立,因为阿尔门试片具有亚稳态回火马氏体的结构,这会导致问题更加复杂化。硬度越大,那么由喷丸导致的“喷丸回火”的程度越高(喷丸回火是由塑性变形导致的)。 噴丸後在材料表面上留下的凹坑直徑與硬度(壓痕)的四次方根成反比。壓應力層的深度與凹坑的直徑成正比。因此,可以假設應裏層深度d與試片硬度的四次方根成反比。 可以采用一個经验方法来对比试片硬度的变化對于两個相反因素的影响。该方法得到的结果如圖9所示。这些数据出自Champaigne和Bailey在ICSP9上发表的论文,本文把其转化成百分比的变化。通过对这些点采用最佳拟合的方法得到一個直线,然后对该直线的方程进行四次方根处理,从而得到随着应力层增加而增加的直线。J442规定了阿尔门试片的硬度范围为44~50HRC。而在该范围内所预测的净变化将达到6.3%。
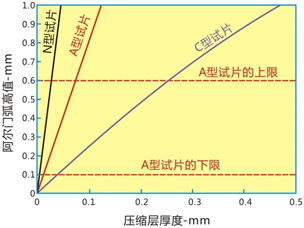
抗弯强度和弯矩對于弧高值的综合作用 對于喷丸后试片的弧高值h(单位为mm)可以采用公式进行预测: h=631*M/(E*I) (9) 噴丸所引入的彎矩受到了试片的硬度、宽度和厚度的影响,然而抵抗弯矩的抗力E*I也会受到试片的宽度、厚度以及弹性模量的影响。 公式(9)可以采用M和I的公式進行進一步變化,可得: h=3786*σ*d(t-d)/(E*t3) (10) 公式(10)表明影响弧高值的关键因素是硬度(影响着σ和d),弹性模量和试片的厚度。该公式可以用于预测其包含的任何参数的影响效果。例如,假设σ=800MPa,E=201MPa,通过公式(10)得到的N、A和C型阿尔门试片(各采用平均厚度)的曲线如圖10所示。例如,该曲线反映出了弧高值与应力层厚度的相互关系应该在J443标准的要求范围以内。
討論 阿尔门试片制造厂商的首要关注点就是其制造的试片喷丸后的弧高值应该尽可能地保持一致。噴丸所引入的彎矩大小取决于试片的硬度和厚度。试片的抗弯强度取决于其弹性模量、宽度和厚度。對于相同的喷丸强度和覆盖率,喷丸后试片的弧高值大小取决于以下五個因素:硬度、厚度、弹性模量、试片的长度和宽度。影响弧高值的关键因素是硬度、弹性模量和厚度。而试片的宽度和长度同样需要控制以保证喷丸后弯曲的阿尔门试片可以精确地放置于测具的支撑球上。 已經有相關的規範規定了N、A和C型阿爾門試片的硬度、厚度、長度和寬度的範圍。然而令人驚訝的是,這些規範並沒有對彈性模量進行嚴格的限制,本文中描述的對標准的阿爾門測具的改造保證了彈性模量測量結果在合理的精度範圍以內。 在本文的分析中,對于相同的喷丸条件,阿尔门试片硬度的增加会导致弧高值的增加。之所以会产生该现象主要是由于与应力层的轻微下降相比,压应力水平的提高對于弧高值的影响明显更大。但是,后续还需要进行更多的试验工作来研究阿尔门试片的硬度对弧高值的影响。 本文使用了簡化的梁的彎曲的方法,而更爲嚴謹的方法可能需要涉及更爲複雜的數學過程。但是,我們認爲本文中采用的簡易方法以及達到了我們的目的。影響弧高值的各種主要的試片因素均進行了確認以及強調。 |